程序员面试题精解(1)— 比特位计数
现代计算机的硬件设计建立于数字电路的基础之上,而数字电路采用以2为基数的二进制记数系统。由此,二进制及其数字位(称为比特)的运算构成计算机系统软件的基石。一个常见的程序员面试题,就是比特位计数,即计算给定整数的二进制表示中比特1的个数。
这并不是一道很难的题目,但是要给出令人印象深刻的答案,却需要对二进制及比特位运算的深入理解,以及坚实的系统编程技巧和经验。实际上,比特位计数功能有悠久的历史。在早期的晶体管计算机时代,就有专门执行该功能的指令。如果主机的CPU指令集不支持此类指令,就必须使用软件代码实现。由于这一功能也常常被称为“种群统计”(population count),本文中所有解法的函数命名都以popcount_为前缀。下面我们来解析和评介这一面试题的各种解法和C语言实现。
常规解法
常规的解法是每一个初级程序员都必须掌握的。以32位整数2418146236为例,
- 十六进制表示:0x9021FBBC
- 二进制表示:0b 10010000 00100001 11111011 10111100
- 比特1的个数:16
如果熟悉基本的比特位运算操作(取反、与、或、异或、左/右移位),就可以很快找到一个解题的思路:生成一个单比特数0b1,将它与要计数的整数做位与运算,结果为1说明整数最右边的比特为1,否则为0;将此单比特数左移一位得到0b10,再与原整数做位与运算,用结果判定从右边起的第二位比特是否为1;重复此左移和位与运算,就能够从右到左扫描到所有的比特1并计数。如下的代码实现了这一简单直接的解法:
1 | int popcount_common1 (uint32_t n) |
可以看到,这种解法的运算量只取决于输入整数类型的总比特数,而与整数本身的数值无关。如上的函数定义,因为输入为32位无符号数,所以代码中循环和移位次数也为32。
与之类似的解法,是固定单比特数0b1,而将输入整数逐次右移,这样所有的高位比特都可以移到最右边来检测。利用比特位右移运算时最左边补上符号位的特点,此解法可能不需要循环32次而提前结束,循环的次数等于最高位比特1与最右边比特的比特距离。以下的代码展示了这一解法:
1 | int popcount_common2 (uint32_t n) |
对于上面的第二种常规解法的C函数实现,有三点要提醒注意:
- 解法利用了右移时最左边补上符号位0的特点,所以可以根据移位后数是否为0,来确定需不需要提前结束循环。这是优于第一种常规解法的地方。但是也由此限定了输入n必须为无符号数,否则当输入为负数时,右移时最左边的符号位会移到数据位,而且还会又补上符号位1。这样最终n会变为0xFFFFFFFF,程序落入死循环!解决此问题的办法是,如果函数定义的输入是
int32_t,要先将之强制类型赋值到无符号数uint32_t,再执行相同的检测和计数步骤。基于此处理,本文余下内容所提到的整数皆为无符号数。 - 以上代码第5行不是应该写成
if (n & 1) c++;吗?为什么变成c += n & 1;?其实两种写法结果一样,但实际中后者可能会优于前者。现代计算机处理器都是基于流水线(pipeline)的设计以提高指令执行速度,而if语句编译成的分支指令,会造成流水线冲突而拉低执行效率。当然,依赖于特定的计算机体系结构和编译器优化能力,这一区别也有可能太小乃至可以忽略不计。 - 以上代码第6行右移一位,等价于将整数除以2。那么请问可以把它写成
n /= 2;吗?绝对不行!这是面试官设置的陷阱。只要学过计算机组成的基础知识,就应该知道除法的执行效率远低于移位运算,所以实际中要尽量避免使用除法。
快速解法
实现常规解法可以验证面试者是否拥有初级程序员的基本技能。然而,对于中高级程序员的职位,面试官会要求效率更高的解法。那么,存在更快的解法吗?答案是肯定的。
考虑一个单字节8比特的整数n, 其数值为0x94,以二进制表示为0b10010100。如下图所示,如果将n减去1,得到0b10010011,即0x93。仔细观察二者的区别,减1后原整数最右边的比特1及后面的比特0全部取反,而其之前的比特位均保持不变。这时,如果将二者做位与运算,结果是0b10010000(0x90),最右的比特1被清除了!重复减1后位与操作,会得到0b10000000 (0x80),原整数从右边数第二个比特1被清除了。第三次同样的操作完成,得到0,即原来的全部三个比特1都被清零。
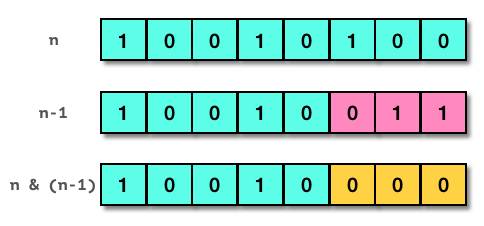
总结这一规律:将一个整数减去1,再同原整数做位与运算,得到的结果等于原整数最右边的比特1清零;在最终结果变成0之前,能重复进行这样的操作的次数,就是原整数中比特1的数目。基于这一规律,我们可以写出新的计数函数代码:
1 | int popcount_fast1 (uint32_t n) |
毫无疑问,由于循环的次数取决于比特1的数目,这种解法当然比常规解法要快。在比特1个数不多的场合,这是优选的快速解法。
无独有偶,还有一种与之对称的解法,适用于比特1个数较多(即比特0较少)的情况。参考下图,整数数值为0xBD,二进制表示为0b10111101。如果将n加上1,得到0b10111110,即0xBE。对比二者,加1后原整数最右边的比特0及后面的比特1全部取反,而其之前的比特位均保持不变。这时,如果将二者做位或运算,结果是0b10111111(0xBF),最右的比特0被置位了!重复加1后位与操作,会得到0b11111111 (0xFF),原整数从右边数第二个比特0被置位了。这时原来的全部两个比特0都被置位,解法终止,原整数中比特1的个数等于总比特数减去重复操作的次数。
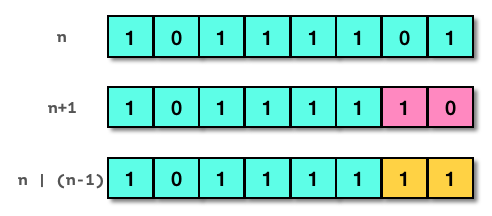
总结新的规律:将一个整数加上1,再同原整数做位或运算,得到的结果等于原整数最右边的比特0置位;在最终结果变成全比特1(等同于有符号数-1)之前,能重复进行这样的操作的次数,就是原整数中比特0的数目,而原整数中比特1的个数等于总比特数减去比特0的数目。这一规律对应的计数函数代码如下:
1 | int popcount_fast2 (uint32_t n) |
同理,由于循环的次数取决于比特0的数目,在比特1个数较多的场合,这是优选的快速解法。
在具体的应用场景中,如果要处理的数据量很大,达到GB甚至TB量级,并且已知绝大部分数值的比特1个数都是较少(或较多)的状况,还可以将循环语句展开,进一步加快运行速度。
以上两种快速解法的循环展开实现如下。代码先定义宏f(x)和g(x)用来检测结果并即时返回计数值,然后在函数实现中拿掉while循环,取而代之的是分别反复调用f(x)和g(x)。在任何一步满足if条件为真,就会马上返回。这实际上是一种以空间换时间的方案。虽然函数代码及编译后的指令数目会增加不少,但是在运行过程中,因为每次检测都减少了一个算术运算指令(用于更新计数变量),所以运行会更快。
1 | /* If most bits are 0, use the following unrolled solution.*/ |
分而治之
如前所述,快速解法是比特1个数较少或较多的情况下的优选。在平均计数值为总比特数的一半时,仍然需要相当多的指令完成任务。对于前例的popcount_fast1和popcount_fast2函数,平均需要循环16次,每次执行三次算术运算和一次比较/分支操作,最少64条操作指令。还有没有更好的、需要更少指令的通用解法呢?
当然有!早在40多年以前,三位美国计算机科学家Reingold、Nievergelt和Deo所著的《组合算法:理论和实践》1一书中,就详细讨论了一种应用“分而治之”(Divide and Conquer)策略的解法。这种解法是如此精妙,乃至应该将其升格以算法称呼才合适。下图演示了以16位的双字节数0xBFA6为例的计算过程,算法首先把相邻的两个比特位组合为一个位段,将这两个比特位的值相加,结果置于这个宽度为2的比特位段中。下一步把相邻的两个双比特位段的值相加,结果置于宽度为4的比特位段中。以此类推,四步之后就得到数值11(0x000B),正好就是原整数中比特1的总数。
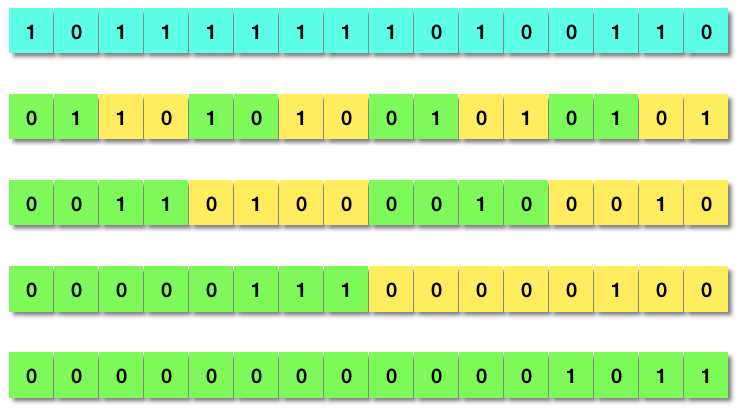
这一看似帽子戏法的算法,是“分而治之”策略的典型应用。一个16位整数的比特1计数问题,被转化为两个8位整数的计数问题,分别解决后再将结果相加合并。递归运用此策略,直至分解到单个比特计数的问题。然后反复运用并行位运算求解再合并,即可求出最终的计数值。很明显,给定N比特位整数,此算法的时间复杂性是\(O(\log N)\)。
对于32位的整数,上图中的算法用C语言写出来就是:
1 | /* Divide-and-Conquer - original (20 arithmetic operations) */ |
值得说明的一点是,此函数实现中的圆括号都是必要的。这是因为在C语言运算符的优先级次序表里,加减(+、-)要高于移位(<<、>>),而后者又高于比特位运算(&、^、|)2。在n >> 1两边加圆括号则有助于增强代码的可读性。
另外,函数的第一行(上面代码段行号4)按照算法描述本来应该写成(n & 0xAAAAAAAA) >> 1,之所以这么写是为了避免在寄存器中生成两个大的常数。如果使用0xAAAAAAAA,在不支持单个“and not”指令的计算机里,就必须多耗费一条指令先将0x55555555取反,再与n做位与运算。后面四行的写法也出于同样的考虑。统计下来,这种“分而治之”算法的实现运算量恒定,总共只有20次算术运算操作,运行速度达到了快速解法平均速度的三倍多!
到这里,如果面试者对以上全部的解法都有清晰的思路并写下无错的代码,应该可以得到面试官的首肯。再往下的知识点,就是属于能给面试官带来惊喜的技能了。
锦上添花
问还可以更快吗?
是的,上述“分而治之”算法的代码实现还能进一步优化:
- 仔细审查函数
popcount_dnq1返回语句之前的三行(代码段行号6、7、8),你会发现一些位与操作是多余的。一则,在这些步骤中比特位段求和的结果不可能向左边的比特位段进位;二则,在最后一步,高位的比特值是可忽略的,计数结果只在最右边的m位比特中,这里\(m=\log N+1\),所以可以省却一个位与运算。 - 函数
popcount_dnq1的第一行(代码段行号4)还有另一种写法,可以减少一次算术运算。其依据是下面的“种群统计”数学公式3: \[\operatorname{popcount}(n)=n-\Bigl\lfloor{\frac{n}{2}}\Bigr\rfloor-\Bigl\lfloor\frac{n}{4}\Bigr\rfloor-\cdots-\Bigl\lfloor\frac{n}{2^{N-1}}\Bigr\rfloor\tag{1}\] N为整数n的比特位数目,\(\lfloor\space\rfloor\)为向下取整操作。此公式的前两项可以用来并行计算宽度为2的比特位段,以一个四比特位数为例: \[\begin{align} n&=a_3⋅2^3+a_2⋅2^2+a_1⋅2^1+a_0⋅2^0\tag{2}\\ \Bigl\lfloor{\frac{n}{2}}\Bigr\rfloor&=a_3⋅2^2+a_2⋅2^1+a_1⋅2^0\tag{3}\\ \Bigl\lfloor{\frac{n}{2}}\Bigr\rfloor\space\&\space0\mathbf{x}5&=a_3⋅2^2+a_1⋅2^0\tag{4}\\ n-(\Bigl\lfloor{\frac{n}{2}}\Bigr\rfloor\space\&\space0\mathbf{x}5)&=a_3⋅(2^3-2^2)+a_2⋅2^2+a_1⋅(2^1-2^0)+a_0⋅2^0\\ &=(a_3+a_2)⋅2^2+(a_1+a_0)⋅2^0\tag{5} \end{align}\] 显然上式(3)等同于将n右移一位。稍加思考,也可以推断出上式(5)得到就是宽度为2的比特位段计数值。依据这一分析,我们可以重写第一行为n = n - ((n >> 1) & 0x55555555);
综合上述两点,优化后的代码如下:
1 | /* Divide-and-Conquer - improved (15 arithmetic operations) */ |
新的popcount_dnq2函数实现比popcount_dnq1少了5个算术运算操作,速度加快了25%。
还有优化的余地吗?
真的有!有经验的系统程序员都知道,许多现代计算机处理器的设计都支持单条乘法指令。由此把一个数乘以0x01010101,等于将其每个长度为8的比特位段相加求和,结果置于最高的字节中,所以只要右移24位就可以得到我们要的计数值。根据这一点,我们可以得到“分而治之”算法的最优实现版本:
1 | /* Divide-and-Conquer - final (12 arithmetic operations) */ |
它只需要12次算术运算操作就完成任务,真的非常快!
使用GCC编译器特定选项,可以生成混合C代码及对照汇编语言的列表(list)文件,用来验证popcount_dnq3实现的优越性。在运行于Intel处理器的Ubuntu Linux x86-64虚拟机上,执行以下命令:
1 | gcc -Wa,-adhln -g -march=native popcount.c > popcount.s |
然后打开产生的列表文件popcount.s,找到popcount_dnq2和popcount_dnq3相关的部分:
1 | 106:popcount.c **** int popcount_dnq2 (uint32_t n) |
可以看到,popcount_dnq2实现里右移8/16位相加各自有三条指令(行号973、974、976和978、979、981),最后的位与0x3F有两条指令(行号983、984),一共8条指令;而在popcount_dnq3实现中只有两条:一条加载指令movl和一条乘法指令imull。popcount_dnq3完胜!
还有一种以空间换时间的“分而治之”方案,虽然看上去比较无趣,但是其执行效率却可与上面的其他算法比肩。这种解决方案预设一个256项的数组,填入0~255之间每个数的比特位计数值,之后对于输入的整数依次取出单个字节查表,然后将结果相加。以下是无比较/分支指令的代码实现:
1 | const char popcount_tab[256] = |
透彻掌握本节的内容,一定可以让面试官对你刮目相看,因为你写出的代码,实现的就是广为认可的高效算法。不信去下载GCC最新的11.1.0版本,看看库文件libgcc/libgcc2.c里的比特位计数函数(复制如下),与前面的代码实质上是一样的:
1 | int |
总结和应用
下表总结比较了本文全部的解法和算法的函数实现:
| 分类 | 函数名 | 方法概要 | 性能 |
|---|---|---|---|
| 常规解法 | popcount_common1 | 从右到左单比特扫描 | 最慢 |
| 常规解法 | popcount_common2 | 输入移位单比特扫描 | 慢 |
| 快速解法 | popcount_fast1 | 减一再位与清零最右1,适用较少1 | 快(非通用) |
| 快速解法 | popcount_fast2 | 加一再位或置位最右0,适用较少0 | 快(非通用) |
| 快速解法 | popcount_fast1_unrolled | fast1循环展开(以空间换时间) | 更快(非通用) |
| 快速解法 | popcount_fast2_unrolled | fast2循环展开(以空间换时间) | 更快(非通用) |
| 分而治之 | popcount_dnq1 | 位段并行计数合并、递归 | 快(通用) |
| 分而治之 | popcount_dnq2 | 位段并行计数合并、递归(优化) | 更快(通用) |
| 分而治之 | popcount_dnq3 | 位段并行计数合并、递归(最优化) | 最快(通用) |
| 分而治之 | popcount_tablelookup | 单字节查表法(以空间换时间) | 最快(通用) |
比特位计数当然不仅仅是用来考验面试者的,它广泛应用于信息学、纠错编码和密码学等多个领域。实际上,“种群统计”就是二进制符号数据的汉明重量4。而两个数据比特串的汉明距离,就定义为二者对应位置上不同比特的个数,即二者相异或后的汉明重量。基于汉明距离的分析是密码分析学的一个关键技术,是历史上破解许多密码的关键。从比特位计数的算法,也衍生出一些快速计算汉明距离的算法,感兴趣者可以留言讨论。
事实上,比特位计数是如此重要,乃至GCC和Clang编译器都提供了内建库函数__builtin_popcount。Intel、AMD和ARM处理器也都为之设定了专门的指令。如下在运行于Intel处理器的Ubuntu Linux x86-64虚拟机上,指定GCC选项-march=native后__builtin_popcount函数编译成单一指令popcntl:
1 | 159:popcount.c **** count = __builtin_popcount(num); |
对比特位计数功能应用方面的了解,有助于扩展知识面,会成为面试时的加分项。
完整程序(包含以上所有计数函数及测试代码)和示例列表文件的压缩包在此下载:popcount.tar.gz