Purdue MA 26500 Spring 2022 Midterm II Solutions
Here comes the solution and analysis for Purdue MA 26500 Spring 2022 Midterm II. This second midterm covers topics in Chapter 4 (Vector Spaces) and Chapter 5 (Eigenvalues and Eigenvectors) of the textbook.
Introduction
Purdue Department of Mathematics provides a linear algebra course MA 26500 every semester, which is mandatory for undergraduate students of almost all science and engineering majors.
Textbook and Study Guide
Disclosure: This blog site is reader-supported. When you buy through the affiliate links below, as an Amazon Associate, I earn a tiny commission from qualifying purchases. Thank you.
MA 26500 textbook is Linear Algebra and its Applications (6th Edition) by David C. Lay, Steven R. Lay, and Judi J. McDonald. The authors have also published a student study guide for it, which is available for purchase on Amazon as well.
Exam Information
MA 26500 midterm II covers the topics of Sections 4.1 – 5.7 in the textbook. It is usually scheduled at the beginning of the thirteenth week. The exam format is a combination of multiple-choice questions and short-answer questions. Students are given one hour to finish answering the exam questions.
Based on the knowledge of linear equations and matrix algebra learned in the book chapters 1 and 2, Chapter 4 leads the student to a deep dive into the vector space framework. Chapter 5 introduces the important concepts of eigenvectors and eigenvalues. They are useful throughout pure and applied mathematics. Eigenvalues are also used to study differential equations and continuous dynamical systems, they provide critical information in engineering design,
Reference Links
- Purdue Department of Mathematics Course Achive
- Purdue MA 26500 Spring 2024
- Purdue MA 26500 Exam Archive
Spring 2022 Midterm II Solutions
Problem 1 (10 points)

Problem 1 Solution
A From the following \[c_1(\pmb u+\pmb v)+c_2(\pmb v+\pmb w)+c_3\pmb w=c_1\pmb u+(c_1+c_2)\pmb v+(c_2+c_3)\pmb w\] it can be concluded that if \(\pmb u\), \(\pmb v\), and \(\pmb w\) are linearly independent, it is always true that \(\pmb u+\pmb v\), \(\pmb v+\pmb w\), and \(\pmb w\) are linearly independent. So this statement is always true.
B This is also true. If the number of vectors is greater than the number of entries (\(n\) here), the transformation matrix has more columns than rows. The column vectors are not linearly independent.
C This is always true per the definition of basis and spanning set.
D If the nullity of a \(m\times n\) matrix \(A\) is zero, \(rank A=n\). This means there the column vectors form a linearly independent set, and there is one pivot in each column. However, this does not mean \(A\pmb x=\pmb b\) has a unique solution for every \(\pmb b\). For example, see the following augmented matrix in row echelon form (after row reduction): \[ \begin{bmatrix}1 &\ast &\ast &b_1\\0 &1 &\ast &b_2\\0 &0 &1 &b_3\\0 &0 &0 &b_4\end{bmatrix} \] If \(b_4\) is not zero, the system is inconsistent and there is no solution. So this one is NOT always true.
E This is always true since the rank of a \(m\times n\) matirx is always in the range of \([0, n]\).
So the answer is D.
Problem 2 (10 points)

Problem 2 Solution
Denote \(3\times 3\) matrix as \(A=\begin{bmatrix}a &b &c\\d &e &f\\g &h &i\end{bmatrix}\), then from the given condition we can get \[\begin{align} &\begin{bmatrix}1 &0 &0\\0 &2 &0\\0 &0 &3\end{bmatrix}\begin{bmatrix}a &b &c\\d &e &f\\g &h &i\end{bmatrix}=\begin{bmatrix}a &b &c\\d &e &f\\g &h &i\end{bmatrix}\begin{bmatrix}1 &0 &0\\0 &2 &0\\0 &0 &3\end{bmatrix}\\ \implies&\begin{bmatrix}a &b &c\\2d &2e &2f\\3g &3h &3i\end{bmatrix}=\begin{bmatrix}a &2b &3c\\d &2e &3f\\g &2h &3i\end{bmatrix}\\ \implies&A=\begin{bmatrix}a &0 &0\\0 &2e &0\\0 &0 &3i\end{bmatrix}=a\begin{bmatrix}1 &0 &0\\0 &0 &0\\0 &0 &0\end{bmatrix}+ 2e\begin{bmatrix}0 &0 &0\\0 &1 &0\\0 &0 &0\end{bmatrix}+ 3i\begin{bmatrix}0 &0 &0\\0 &0 &0\\0 &0 &1\end{bmatrix} \end{align}\]
It can be seen that there are three basis vectors for this subspace and the dimension is 3. The answer is A.
Notice the effects of left-multiplication and right-multiplication of a diagonal matrix.
Problem 3 (10 points)
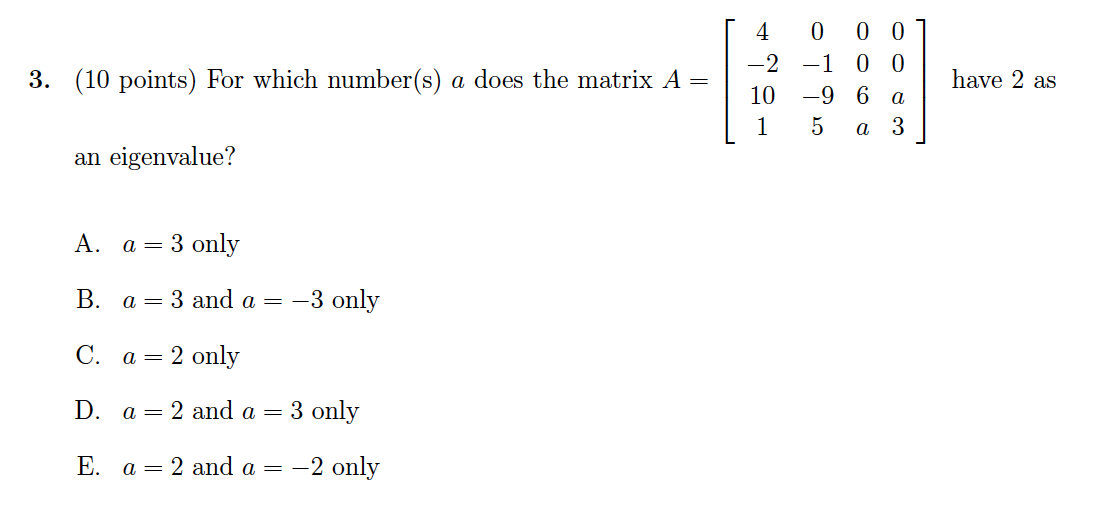
Problem 3 Solution
From \(\det A-\lambda I\), it becomes \[\begin{align} \begin{vmatrix}4-\lambda &0 &0 &0\\-2 &-1-\lambda &0 &0\\10 &-9 &6-\lambda &a\\1 &5 &a &3-\lambda\end{vmatrix} &=(4-\lambda)(-1-\lambda)((6-\lambda)(3-\lambda)-a^2)\\ &=(\lambda-4)(\lambda+1)(\lambda^2-9\lambda+18-a^2) \end{align}\]
So if 2 is an eigenvalue for the above, the last multiplication item becomes \((2^2-18+18-a^2)\) that should be zero. So \(a=\pm 2\).
The answer is E.
Problem 4 (10 points)

Problem 4 Solution
(i) Referring to Theorem 4 in Section 5.2 "The Characteristic Equation" >If \(n\times n\) matrices \(A\) and \(B\) are similar, then they have the same characteristic polynomial and hence the same eigenvalues (with the same multiplicities).
So this statement must be TRUE.
(ii) If the columns of \(A\) are linearly independent, \(A\pmb x=\pmb 0\) only has trivial solution and \(A\) is an invertible matrix. This also means \(\det A\neq 0\). From here, it must be TRUE that \(\det A-0 I\neq 0\). So 0 is NOT an eigenvalue of \(A\). This statement is FALSE.
(iii) A matrix \(A\) is said to be diagonalizable if it is similar to a diagonal matrix, which means that there exists an invertible matrix \(P\) such that \(P^{-1}AP\) is a diagonal matrix. In other words, \(A\) is diagonalizable if it has a linearly independent set of eigenvectors that can form a basis for the vector space.
However, the condition for diagonalizability does not require that all eigenvalues be nonzero. A matrix can be diagonalizable even if it has one or more zero eigenvalues. For example, consider the following matrix: \[A=\begin{bmatrix}1 &0\\0 &0\end{bmatrix} =\begin{bmatrix}1 &0\\0 &1\end{bmatrix}\begin{bmatrix}1 &0\\0 &0\end{bmatrix}\begin{bmatrix}1 &0\\0 &1\end{bmatrix}\] This matrix has one nonzero eigenvalue (\(λ = 1\)) and one zero eigenvalue (\(λ = 0\)). However, it is diagonalizable with the identity matrix as \(P\) and \(D=A\).
So this statement is FALSE.
(iv) Similar matrices have the same eigenvalues (with the same multiplicities). Hence \(-\lambda\) is also an eigenvalue of \(B\). Then we have \(B\pmb x=-\lambda\pmb x\). From this, \[ BB\pmb x=B(-\lambda)\pmb x=(-\lambda)B\pmb x=(-\lambda)(-\lambda)\pmb x=\lambda^2\pmb x \] So \(\lambda^2\) is an eigenvalue of \(B^2\). Following the same deduction, we can prove that \(\lambda^4\) is an eigenvalue of \(B^4\). This statement is TRUE.
(v) Denote \(A=PBP^{-1}\). If \(A\) is diagonizible, then \(A=QDQ^{-1}\) for some diagonal matrix \(D\). Now we can also write down \[B=P^{-1}AP=P^{-1}QDQ^{-1}P=(P^{-1}Q)D(P^{-1}Q)^{-1}\] This proves that \(B\) is also diagonalizable. This statement is TRUE.
Since statements (ii) and (iii) are FALSE and the rest are TRUE, the answer is D.
Problem 5 (10 points)

Problem 5 Solution
(i) Obviously \(x=y=z=0\) does not satisfy \(x+2y+3z=1\), this subset is NOT a subspace of \(\mathbb R^3\).
(ii) This subset is a subspace of \(\mathbb R^3\) since it has all the three properties of subspace:
- Be \(x=y=z=0\) satisfies \(10x-2y=z\), so the set includes the zero vector.
- Because \(10(x_1+x_2)-2(y_1+y_2)=z_1+z_2\), it is closed under vector addition.
- \(10cx-2cy=cz\), it is closed under scalar multiplication as well.
(iii) Here \(p(t)=a_0+a_1t+a_2t^2+a_3t^3\) and \(a_3\neq 0\). This set does not include zero polynomial. Besides, if \(p_1(t)=t^3+t\) and \(p_2(t)=-t^3+t\), then \(p_1(t)+p_2(t)=2t\). This result is not a polynomial of degree 3. So this subset is NOT closed under vector addition and is NOT a subspace of \(\mathbb P_3\).
(iv) The condition \(p(2)=0\) means \(a_0+2a_1+4a_3+8a_3=0\). It does include zero polynomial. It also satisfies the other two properties because \[\begin{align} cp(2)&=c(a_0+2a_1+4a_3+8a_3)=0\\ p_1(2)+p_2(2)&=(a_0+2a_1+4a_3+8a_3)+(b_0+2b_1+4b_3+8b_3)=0 \end{align}\] So this set is indeed a subset of \(\mathbb P_3\).
Since we have (ii) and (iv) be our choices, the answer is A.
Problem 6 (10 points)

Problem 6 Solution
\[ \begin{vmatrix}4-\lambda &2\\3 &5-\lambda\end{vmatrix}=\lambda^2-9\lambda+20-6=(\lambda-2)(\lambda-7) \]
So there are two eigenvalues 2 and 7. Since both are positive, the origin is a repeller. The answer is B.
Problem 7 (10 points)

Problem 7 Solution
From Section 5.7 "Applications to Differential Equations", we learn that the general solution to a matrix differential equation is \[\pmb x(t)=c_1\pmb{v}_1 e^{\lambda_1 t}+c_2\pmb{v}_2 e^{\lambda_2 t}\] For a real matrix, complex eigenvalues and associated eigenvectors come in conjugate pairs. The real and imaginary parts of \(\pmb{v}_1 e^{\lambda_1 t}\) are (real) solutions of \(\pmb x'(t)=A\pmb x(t)\), because they are linear combinations of \(\pmb{v}_1 e^{\lambda_1 t}\) and \(\pmb{v}_2 e^{\lambda_2 t}\). (See the proof in "Complex Eigenvalues" of Section 5.7)
Now use Euler's formula (\(e^{ix}=\cos x+i\sin x\)), we have \[\begin{align} \pmb{v}_1 e^{\lambda_1 t} &=e^{1+i}\begin{bmatrix}1-2i\\3+4i\end{bmatrix}\\ &=e^t(\cos t+i\sin t)\begin{bmatrix}1-2i\\3+4i\end{bmatrix}\\ &=e^t\begin{bmatrix}\cos t+2\sin t+i(\sin t-2\cos t)\\3\cos t-4\sin t+i(3\sin t+4\cos t)\end{bmatrix} \end{align}\] The general REAL solution is the linear combination of the REAL and IMAGINARY parts of the result above, it is \[c_1 e^t\begin{bmatrix}\cos t+2\sin t\\3\cos t-4\sin t\end{bmatrix}+ c_2 e^t\begin{bmatrix}\sin t-2\cos t\\3\sin t+4\cos t\end{bmatrix}\]
The answer is A.
Problem 8 (10 points)
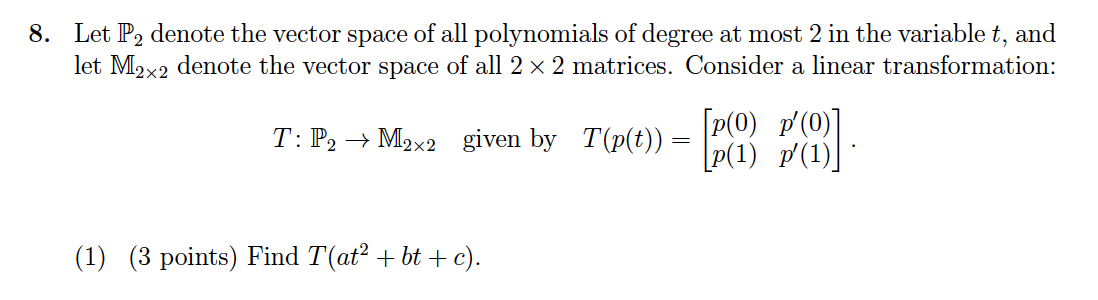
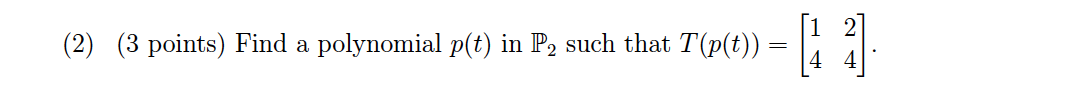
Problem 8 Solution
(1) Since \(p(t)=at^2+bt+c\), its derivative is \(p'(t)=2at+b\). So we can have \[ T(at^2+bt+c)=\begin{bmatrix}c &b\\a+b+c &2a+b\end{bmatrix} \]
(2) From the result of (1) above, we can directly write down that \(c=1\) and \(b=2\). Then because \(2a+b=4\), \(a=2\). So \(p(t)=t^2+2t+1\).
(3) Write down this transformation as the parametric vector form like below \[ \begin{bmatrix}c &b\\a+b+c &2a+b\end{bmatrix}= a\begin{bmatrix}0 &0\\1 &2\end{bmatrix}+ b\begin{bmatrix}0 &1\\1 &1\end{bmatrix}+ c\begin{bmatrix}1 &0\\1 &0\end{bmatrix} \] So a basis for the range of \(T\) is \[ \begin{Bmatrix} \begin{bmatrix}0 &0\\1 &2\end{bmatrix}, \begin{bmatrix}0 &1\\1 &1\end{bmatrix}, \begin{bmatrix}1 &0\\1 &0\end{bmatrix} \end{Bmatrix} \]
Problem 9 (10 points)

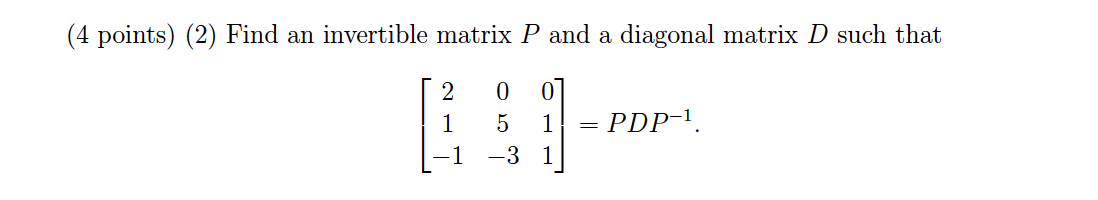
Problem 9 Solution
(1) First find all the eigenvalues using \(\det A-\lambda I=0\) \[ \begin{align} \begin{vmatrix}2-\lambda &0 &0\\1 &5-\lambda &1\\-1 &-3 &1-\lambda\end{vmatrix}&=(2-\lambda)\begin{vmatrix}5-\lambda &1\\-3 &1\lambda\end{vmatrix}\\ &=(2-\lambda)(\lambda^2-6\lambda+5+3)\\ &=(2-\lambda)(\lambda-2)(\lambda-4) \end{align} \] So there are two eigenvalues 2 with multiplicity and 4.
Now find out the eigenvector(s) for each eigenvalue
For \(\lambda_1=\lambda_2=2\), the matrix \(\det A-\lambda I\) becomes \[ \begin{bmatrix}0 &0 &0\\1 &3 &1\\-1 &-3 &-1\end{bmatrix}\sim \begin{bmatrix}0 &0 &0\\1 &3 &1\\0 &0 &0\end{bmatrix} \] Convert this result to a parametric vector form with two free variables \(x_2\) and \(x_3\) \[ \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}= \begin{bmatrix}-3x_2-x_3\\x_2\\x_3\end{bmatrix}= x_2\begin{bmatrix}-3\\1\\0\end{bmatrix}+x_3\begin{bmatrix}-1\\0\\1\end{bmatrix} \] So the basis for the eigenspace is \(\begin{Bmatrix}\begin{bmatrix}-3\\1\\0\end{bmatrix},\begin{bmatrix}-1\\0\\1\end{bmatrix}\end{Bmatrix}\).
For \(\lambda_3=4\), the matrix \(\det A-\lambda I\) becomes \[ \begin{bmatrix}-2 &0 &0\\1 &1 &1\\-1 &-3 &-3\end{bmatrix}\sim \begin{bmatrix}1 &0 &0\\0 &1 &1\\0 &-2 &-2\end{bmatrix}\sim \begin{bmatrix}1 &0 &0\\0 &1 &1\\0 &0 &0\end{bmatrix} \] This ends up with \(x_1=0\) and \(x_2=-x_3\). So the eigenvector is \(\begin{bmatrix}0\\-1\\1\end{bmatrix}\) or \(\begin{bmatrix}0\\1\\-1\end{bmatrix}\). The basis for the corresponding eigenspace is \(\begin{Bmatrix}\begin{bmatrix}0\\-1\\1\end{bmatrix}\end{Bmatrix}\) or \(\begin{Bmatrix}\begin{bmatrix}0\\1\\-1\end{bmatrix}\end{Bmatrix}\).
(2) From the answers of (1), we can directly write down \(P\) and \(D\) as \[ P=\begin{bmatrix}-3 &-1 &0\\1 &0 &-1\\0 &1 &1\end{bmatrix},\; D=\begin{bmatrix}2 &0 &0\\0 &2 &0\\0 &0 &4\end{bmatrix} \]
Problem 10 (10 points)
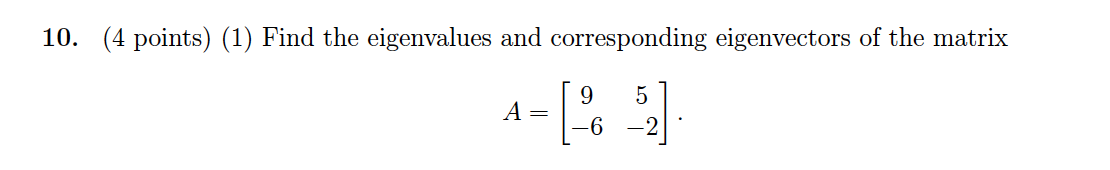

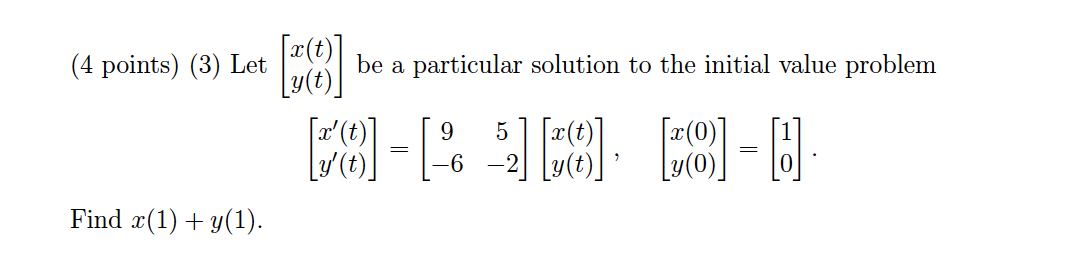
Problem 10 Solution
(1) First find the eigenvalues using \(\det A-\lambda I=0\) \[ \begin{align} \begin{vmatrix}9-\lambda &5\\-6 &-2-\lambda\end{vmatrix} &=\lambda^2-7\lambda-18-(-5)\cdot 6\\ &=\lambda^2-7\lambda+12\\ &=(\lambda-3)(\lambda-4) \end{align} \] So there are two eigenvalues 3 and 4.
For \(\lambda_1=3\), the matrix \(\det A-\lambda I\) becomes \[ \begin{bmatrix}6 &5\\-6 &5\end{bmatrix}\sim \begin{bmatrix}6 &5\\0 &0\end{bmatrix} \] So the eigenvector can be \(\begin{bmatrix}-5\\6\end{bmatrix}\).
Likewise, for \(\lambda_2=4\), the matrix \(\det A-\lambda I\) becomes \[ \begin{bmatrix}5 &5\\-6 &-6\end{bmatrix}\sim \begin{bmatrix}1 &1\\0 &0\end{bmatrix} \] So the eigenvector can be \(\begin{bmatrix}-1\\1\end{bmatrix}\).
(2) With the eigenvalues and corresponding eigenvectors known, we can apply them to the general solution formula \[\pmb x(t)=c_1\pmb{v}_1 e^{\lambda_1 t}+c_2\pmb{v}_2 e^{\lambda_2 t}\] So the answer is \[ \begin{bmatrix}x(t)\\y(t)\end{bmatrix}=c_1\begin{bmatrix}-5\\6\end{bmatrix}e^{3t}+c_2\begin{bmatrix}-1\\1\end{bmatrix}e^{4t} \]
(3) Apply the initial values of \(x(0)\) and \(y(0)\), here comes the following equations: \[\begin{align} -5c_1-c_2&=1\\ 6c_1+c_2&=0 \end{align}\] This gives \(c_1=1\) and \(c_2=-6\). So \(x(1)+y(1)=-5e^{3}+6e^4+6e^3-6e^4=e^3\).

